Jan 16, 2024

LDPC编码与译码

LDPC码编码与译码实现

摘要

作为线性分组码的一种，LDPC码在1962年由Gallager提出。其纠错能力被证明可以接近香农极限。由于设备性能限制，在当时LDPC码并未广泛普及。随着近年集成电路技术与嵌入式计算技术的发展，LDPC码的广泛应用逐渐有了较强的可行性。本文将基于LDPC码的基本原理，介绍LDPC码编码原理与实现，基于LLR函数的LDPC码译码(Sum-Product Algorithem)实现，并尝试利用matlab配合2PSK调制方法实现了一个简单的仿真模型，以及基于蒙特卡洛分析的性能仿真

LDPC编码理论

LDPC码属于线性分组码，其编码方式与普通的线性分组码编码方式没有区别。这里主要介绍H矩阵的构造方法。

H矩阵须满足一个基本原则，即“每行的行重一致，每列列重一致，且每两列相同位置均为1的个数不超过1，以及行重与列重和H矩阵中的列数和行数相比需小得多。”

在Gallager初始的研究中，校验矩阵的构建往往遵从随机原则。随着时代的发展，学者们更倾向于利用现代代数的理论来描述构建H矩阵。结合诸如凸优化等优化方法，LDPC码可以无限接近香农极限。

H矩阵构造

考虑一个具有一般性的LDPC码校验矩阵构造，出于实用角度出发，我们选择CCSDS document (version 1,published in 2006)中的方法构造校验矩阵，该方法构造的校验矩阵可以适用不同的编码效率，具有较强的通用性。

以码率为1/2的H矩阵构造为例，首先需确定参数M，根据M可构建出M*M大小的子矩阵，子矩阵往往由零矩阵 $0_M$ ，单位矩阵 $I_M$ 和置换矩阵 $\Pi _M$ 构成。对于置换矩阵 $\Pi _M$ ，其构造遵循下述公式：

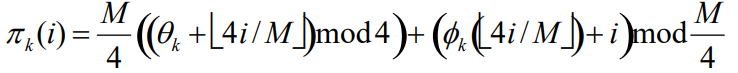
Untitled

其中 $\theta _k$ 和 $\phi_k$ 的值可以由一个单独的表确定

则1/2码率的校验矩阵可以通过下述矩阵表示

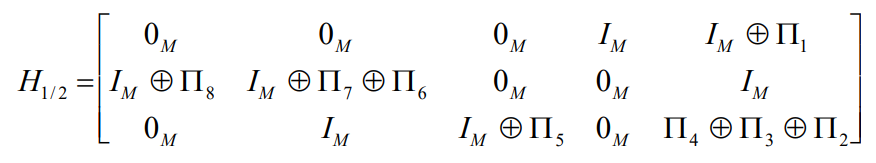
Untitled

根据上述理论，可以得到如下代码

function [ H ] = checkmatrix( M ,RATE )

theta=[1  1  2  3  1  1  2  3  1  2  3  0  2  3  0  2  3  0  1  3  0  1  3  0  1  2];
fai=[1787  1077  1753  697  1523  5  2035  331  1920  130  4  85  551  15  1780  1960  3  145  1019  691  132  42  393  502  201  1064
1502  602  749  1662  1371  9  131  1884  1268  1784  19  1839  81  2031  76  336  529  74  68  186  905  1751  1516  1285  1597  1712
1887  521  590  1775  1738  2032  2047  85  1572  78  26  298  1177  1950  1806  128  1855  129  269  1614  1467  1533  925  1886  2046  1167
1291  301  1353  1405  997  2032  11  1995  623  73  1839  2003  2019  1841  167  1087  2032  388  1385  885  707  1272  7  1534  1965  588];

A = zeros(M);
B = eye(M);

L = 0:M-1;
for matrixNum = 1:26
    t_k = theta(matrixNum);
    f_4i_M = floor(4*L/M);
    f_k = fai(f_4i_M+1,matrixNum)';
    col_1 = M/4*(mod((t_k+f_4i_M),4)) + ...
        mod((f_k+L),M/4);
    row_col = col_1+1 + L*M;
    C_temp = zeros(M);
    C_temp(ind2sub([M,M],row_col)) = 1;
    C{matrixNum} = C_temp';
end

H = [A A A B B+C{1};B+C{8} B+C{7}+C{6} A A B;A B B+C{5} A C{4}+C{3}+C{2}];

switch(RATE)
    case 1/2
        H=H;
        gridCol = 1:4;
    case 2/3
        H_23 = [A A;B C{11}+C{10}+C{9};C{14}+C{13}+C{12} B];
        H=[H_23 H];
        gridCol = 1:6;
    case 4/5
        H_23 = [A A;B C{11}+C{10}+C{9};C{14}+C{13}+C{12} B];
        H_45 = [A A A A;B C{23}+C{22}+C{21} B C{17}+C{16}+C{15};...
            C{26}+C{25}+C{24} B C{20}+C{19}+C{18} B];
        H = [H_45 H_23 H];
        gridCol = 1:10;
end

end

在获得校验矩阵后，通过列变换不难得到系统形式的校验矩阵，以及系统形式的生成矩阵。最后根据线性分组码的一般方法，便可以完成LDPC码的编码。

LDPC码解码

对于LDPC码解码，其软解码开销往往高于硬解码，但是却具有远超硬解码的纠错与译码性能。下面考虑一个AWGN信道下，LDPC码基于Sum-Product Algorithem的解码过程

我们不妨假设AWGN的方差是 $\sigma ^2$ ，令发送信号为 $U$ ，接收信号为 $Y$ ，

对于信道传输后x=0和x=1的概率，我们可以得到LLR函数。

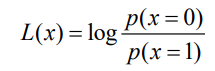
Untitled

由AWGN信道数学性质可以得到：

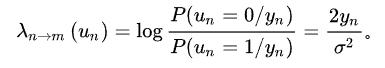
Untitled

上述公式表述了发送端发送比特为0/1的后验概率。由于概率域上的连乘操作会消耗大量算力，故转化为对数域，将乘法运算转化为加法运算。

利用Tanner图我们可以比较便利的表示一个线性分组码

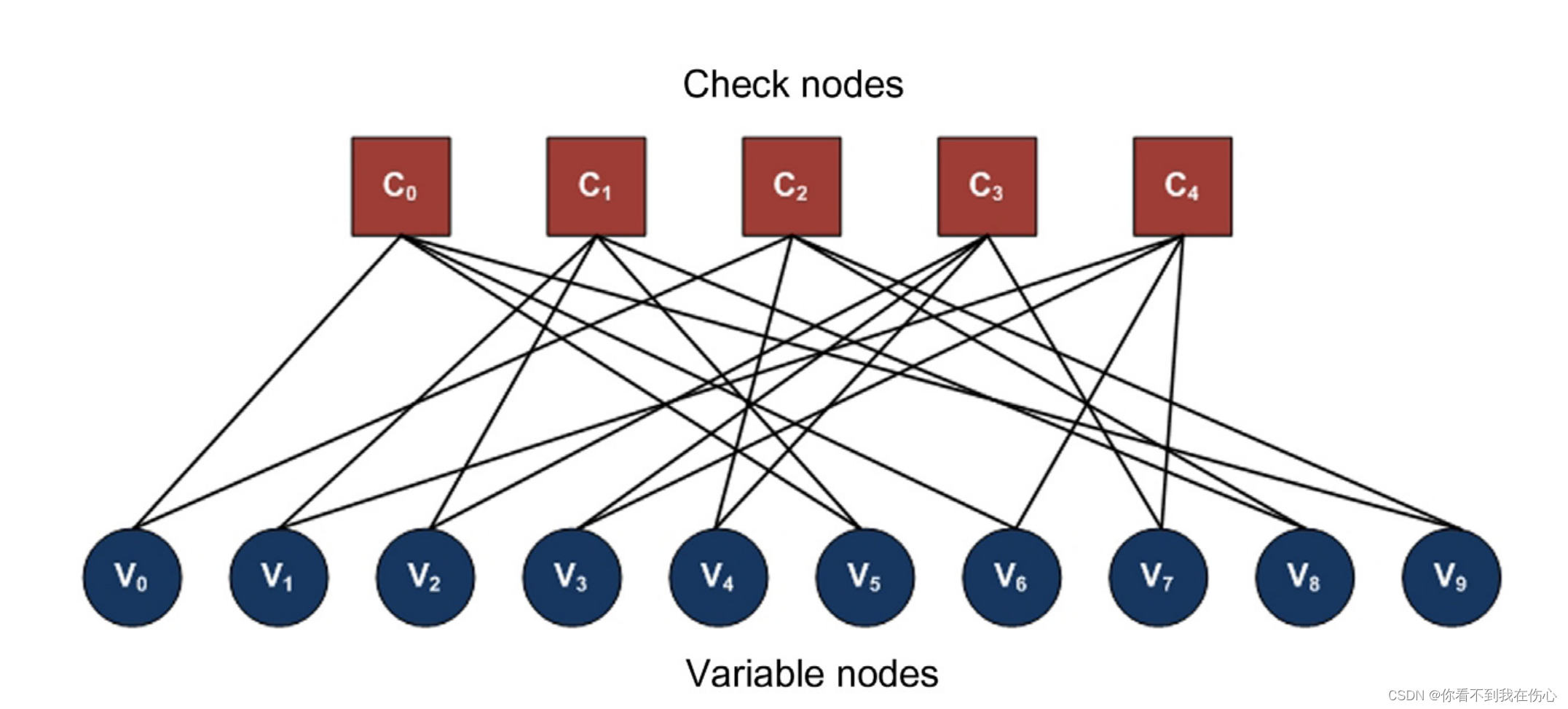
Untitled

考虑任意校验节点 $c_j$ ，与其连接的变量节点 $v_i$ 的值确定，且除 $v_i$ 外其他变量节点为0或者1的概率已知的条件下，我们可以得到第 $j$ 个校验方程满足的概率。上述公式我们得到了任意比特经过AWGN信道传输后的后验概率，结合上述公式我们不难得到第 $j$ 个校验方程满足的概率，即校验节点传递给变量的外信息为：

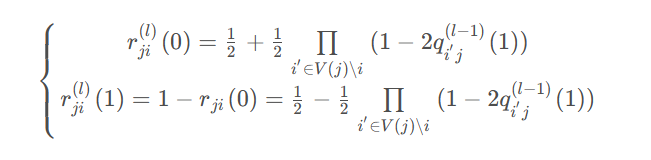
Untitled

对每个变量节点进行遍历，计算变量节点传递给校验节点的外信息，并将概率值相乘，便得到了任意变量节点经过信道传输后的后验概率。

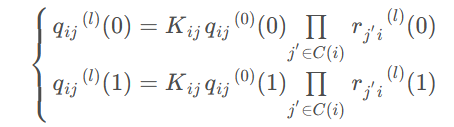
Untitled

若0的概率大，判决为1。否则判决为0

考虑到对于大多数硬件实现乘法计算开销较大，我们选择将概率域转化到对数域。这样连乘操作便转化为了计算开销更小的连加操作。

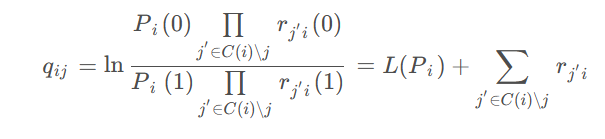
Untitled

在上述理论的基础下，我们便得到了基于Sum-Product算法的一般性LDPC码译码方法。利用matlab有以下具体实现：

function [ iter,decoderData ] = ldpcdecoderllr(H,HRowNum,HColNum,receiveSignal,SNR,MAX_ITER_NUM)
%LDPCC decode algorithm , based on the log-likelihood ratio algorithm
% H: check matrix
% HRowNum,HColNum: index generate from check matrix
% receiveSignal: received soft information from channel
% SNR: signal-to-noise-ration, used to derive metric
% MAT_INTER_NUM: maximum iterations
% HRowNum,HColNum generating by the following codes
%   [r_mark,c_mark] = find(H~=0);
%   HColNum = sum(H);
%   HRowNum = cell(1,size(H,1));
%   for rowH = 1:size(H,1)
%     HRowNum{rowH} = find(r_mark==rowH);
%   end

% The structure of this function is the same as ldpcdecoderminsum

[~,N] = size(H);

vl = 2*receiveSignal*SNR;
decoderData = zeros(1,N);

uml = zeros(1,sum(HColNum));
vml = uml;
ColStart = 1;
for L=1:length(HColNum)
    vml(ColStart:ColStart+HColNum(L)-1) = vl(L);
    ColStart = ColStart+HColNum(L);
end

for iter=1:MAX_ITER_NUM

    for L=1:length(HRowNum)
        L_col = HRowNum{L};
        vmltemp = vml(L_col);
        vmlMark = ones(size(vmltemp));
        vmlMark(vmltemp<0) = -1;
        vmlMark = prod(vmlMark);
        vmltemp1 = (exp(abs(vmltemp))+1)./(exp(abs(vmltemp))-1+eps);
        faitemp = sum(log(vmltemp1+eps));
        for L_col_i = 1:length(L_col)
            vmltemp2 = (exp(abs(vmltemp(L_col_i)))+1)/...
                (exp(abs(vmltemp(L_col_i)))-1+eps);
            vmltemp2 = log(vmltemp2+eps);
            vmltemp3 = faitemp-vmltemp2;
            vmltemp3 = log((exp(vmltemp3)+1)/(exp(vmltemp3)-1+eps)+eps);
            if vmltemp(L_col_i)<0
              vmltemp(L_col_i) = -vmlMark*vmltemp3;
            else
              vmltemp(L_col_i) = vmlMark*vmltemp3;
            end
        end
        uml(L_col) = vmltemp;
    end

    ColStart = 1;
    qn0_1 = ones(1,N);
    for L=1:length(HColNum)
        umltemp = uml(ColStart:ColStart+HColNum(L)-1);
        temp = sum(umltemp);
        qn0_1(L) = temp + vl(L);
        umltemp = temp - umltemp;
        vml(ColStart:ColStart+HColNum(L)-1) = umltemp + vl(L);

        ColStart = ColStart+HColNum(L);
    end


    decoderData(qn0_1>=0) = 0;
    decoderData(qn0_1<0) = 1;
    if(mod(H*decoderData',2)==0)
        break;
    end
end

仿真模型构建

本文基于matlab以及PSK调制方式构建了一套仿真模型。利用蒙特卡洛模拟的思想随机生成一系列的初始码元，并对其进行LDPC编码。对初始信息码元利用2PSK调制，在不同给定SNR下通过AWGN信道传输，在接受端进行2PSK解调后利用和积算法译码，得到还原后的码元。最后将还原后的码元与原始信息码元按位与或，便可以得到不同SNR下LDPC码的误码率表。流程图如下图所示：

幻灯片1.PNG

仿真结果

Untitled