Nov 3, 2023

扩频调制

摘要

以下内容来自gpt

基于伪随机码序列的扩频通信是一种特殊的无线通信技术，其基本思想是使用一个与信息信号无关的伪随机码序列来对信息信号进行“扩频”。

扩频技术的核心：扩频通信的主要思想是将窄带信息信号扩展成宽带信号进行传输。这样做的好处是能够增加信号的鲁棒性、减少干扰和窃听，以及提高频谱效率。
伪随机码序列：伪随机码序列，也称为扩频码或扩频序列，是一种与信息信号无关的、具有随机性的码序列。尽管它看起来像随机序列，但它是完全可预测和可重复的。常见的伪随机码包括Gold码、M序列、Walsh码等。
信息信号的扩频：在发送端，信息信号与伪随机码进行特定的运算（如异或操作），使得信息信号被扩展到更宽的频率范围。这个经过扩频处理的信号将在频谱上占用比原始信号更大的带宽。
信号的接收和解扩：在接收端，使用与发送端相同的伪随机码序列对接收到的信号进行解扩操作。这个过程实质上是将扩频的信号还原回其原始的窄带信息信号。只有知道正确的伪随机码序列的接收者才能成功地解扩并恢复出原始信号，这为通信提供了一定程度的安全性。
抗干扰和抗多径特性：由于扩频信号在频谱上的带宽比原始信号大得多，因此它对短时间、窄带的干扰具有很好的抗干扰性。此外，扩频技术还可以抵御多径干扰，这在无线通信中是一个常见的问题。
使用场景：扩频通信技术被广泛应用于军事通信、移动通信、无线局域网和全球定位系统（GPS）等领域。

总结：基于伪随机码序列的扩频通信是一种将窄带信息信号扩展到宽带频谱上的通信技术，它能够提高信号的鲁棒性、增加通信的安全性，并具有良好的抗干扰和抗多径特性。

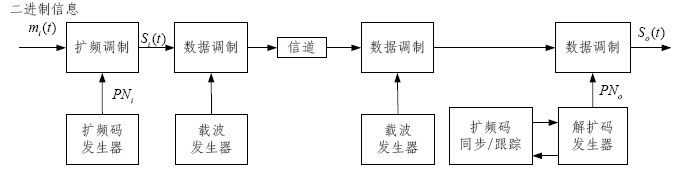
Untitled

本文基于直接扩频技术的原理，通过伪随机序列发生器与数字乘法器，完成了系统建模，并在matlab下实现了系统仿真

理论基础

香农定理告诉我们基于香农原理的信道容量公式:

C=B\log_2(1+\frac{S}{N})

考虑一个特殊的情况下，当噪声功率远大于信号功率时，即在信号淹没在噪声中的情况时（S/N<<1），可以运用自然对数变化将式，有:（换底公式）

C=B\times1.44\ln\biggl(1+\frac{S}{N}\biggr)

利用幂级数展开（等价无穷小），略去高次项可得到

C=B\times1.44\ln\frac{S}{N}

由此可知在已知信噪比与需要的信道容量的前提下，根据上式可以求得需要的信道带宽。

基于上述结果，我们不难发现，想要对抗噪声功率的增加，可以考虑在不改变信号功率的前提下增大带宽 $B$ ，便可以实现高鲁棒性传输。

伪随机序列与m序列

我们都知道随机噪声会使信号产生误码与干扰，我们通常希望减小随机噪声。但是从另一个角度来说，随机信号往往具有丰富的频率分量与极宽的频带。在扩频通信中我们利用随机噪声的上述特性来实现我们频域的拓展。为达成这点，首先我们先要获得一个伪随机序列。

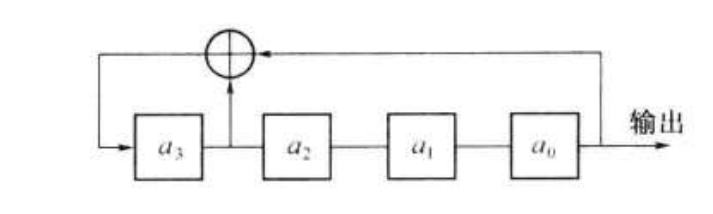
Untitled

最常用的伪随机序列之一便是m序列。这是一种由带线性反馈的移位寄存器产生的周期最长序列。首先考虑一个四级线性反馈移位寄存器，其初始状态我们设为 $(a_3,a_2,a_1,a_0)=(1,0,0,0)$ ，每次移位我们都将最低位与最高位做模2加（xor）运算，并将结果作为最新的 $a_3$ 。不难发现这是一个周期为15的向量，供 $2^{4}=16$ 中可能的状态不断循环。

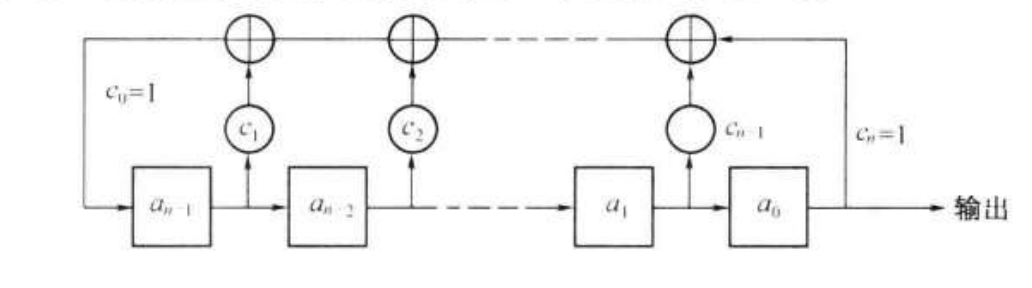
将上述结构扩展成n级，并在每一级加入异或门，则最长周期不难发现为 $2^n-1$ 。这时候我们便构建出了一个伪随机序列生成器。详细数学证明参见《通信原理》p394。

Untitled

基于m序列的直接扩频实现与数学原理

上面提到的m序列，其特征类似于高斯函数。在通信系统中，对于数字基带信号 $s(t)$ ，我们将该信号转化成双极码的形式 $s_b(t)$ 。将其与同样是双极码形式的m序列 $n(t)$ 相乘，得到的是扩频后的信号。

从数字信号角度考虑，假设生成的m序列为 $n(t)=[-1,1,1,-1]$ 。令 $s_o(t)=s_b(t)n(t)$ ，由此可得到扩频后的信号。解扩的过程就是简单的 $s_b(t)=s_o(t)n(t)$ 。也就是

s_b(t)=s_b(t)n(t)n(t)

由于

n(t)n(t)=[-1 \times-1,1 \times 1, 1 \times 1, -1 \times -1]=[1,1,1,1]

不难发现上式必成立。

从信号与通信原理角度来说，时域上相同PN序列相乘相当于频域上相同PN序列做卷积。由自相关函数的对偶性可知，上述操作本质上便是求频域上的自相关函数。同一信号相关性最大 $R(0)$ ，此时功率谱能量集中于零点附近。相当于构建了一个针对低频基带信号的滤波器。

系统模型与实现

本文在数字基带的基础上，通过伪随机序列发生器与乘法器，实现了数字基带信号的扩频调制。具体代码如下所示。

clc;
clear all;

%参数定义
Fs = 1000;
fc = 100;
fp = 10; %扩频因子

m_og = [0 0 1 1 1 1 0 0]; %原始序列消息
for i = 1:length(m_og)
   if(m_og(i)==0)
        m_og(i) = -1;
   end
end
%生成基带信号(双极性非归零码)
m_bi_polar = repmat(m_og,fp,1);
m_bi_polar = reshape(m_bi_polar,1,[]);

%生成随机序列，与基带信号相乘
pn_code = randi([0,1],1,length(m_og)*fp);
for i = 1:length(pn_code)
    if(pn_code(i) == 0)
        pn_code(i) = -1;
    end
end
relate_pn = pn_code.*pn_code;
DSSS = m_bi_polar.*pn_code;
%时域上相同PN序列相乘相当于频域上相同PN序列做卷积
%由自相关函数的对偶性可知，上述操作本质上便是求频域上的自相关函数
%同一信号相关性最大为R(0),此时功率谱能量集中于零点附近
%相当于构建了一个针对低频基带信号的滤波器
%信号还原，分别尝试使用正确的随机序列与错误的随机序列进行解调
pn_code_wrong = randi([0,1],1,length(DSSS));
for i = 1:length(pn_code_wrong)
    if(pn_code_wrong(i) == 0)
        pn_code_wrong(i) = -1;
    end
end
DSSS_rx1 = DSSS.*pn_code;
DSSS_rx2 = m_bi_polar.*pn_code_wrong;

%查看变换后信号频谱
fft_base = abs(fftshift(fft(m_bi_polar,1024)));
fft_pn = abs(fftshift(fft(pn_code,1024)));
fft_DSSS = abs(fftshift(fft(DSSS_rx1,1024)));
fft_relate_pn = abs(fftshift(fft(relate_pn,1024)));

参考文献

200305018.pdf (nudt.edu.cn)